Category: Funções com radicais
Funções com radicais: Aleph 11 - Volume 2 Pág. 177 Ex. 11
Enunciado
Dois automóveis circulam à mesma velocidade, em estradas perpendiculares, em direção a um cruzamento.
Um deles encontra-se a $5$ km do cruzamento e o outro a $6$ km.
Representa graficamente a função que dá a distância entre os dois automóveis à medida que se aproximam do cruzamento.
Utilizando a calculadora gráfica, determina quando é que a distância entre os automóveis é mínima.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Aleph 11 - Volume 2 Pág. 177 Ex. 10
Enunciado
Considere uma folha de papel retangular de comprimento 24 unidades e largura 18 unidades.
Dobramos a folha de papel de modo que o vértice A coincida com o vértice C e vincamos a folha.
Qual é o comprimento do vinco?
- Sugestão: Comece por dobrar uma folha de papel retangular e descubra as relações entre os vários elementos geométricos.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Aleph 11 - Volume 2 Pág. 174 Ex. 16
Enunciado
Considere o triângulo da figura inscrito numa semicircunferência de centro C.
- Justifique que o triângulo é retângulo.
- Exprima a área do triângulo em função do raio e do cateto de comprimento $x$.
- Qual deve ser o raio da circunferência para que o triângulo tenha área $10$ e um cateto seja duplo do outro?
- Se o raio for igual a $5$, qual é a maior área do triângulo inscrito?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Aleph 11 - Volume 2 Pág. 174 Ex. 12
Enunciado
Simplifica as seguintes expressões com radicais:
- ${ – \sqrt[3]{2} + 2\sqrt[3]{2} + 3\sqrt[2]{2}}$
- $\frac{{\sqrt {45} }}{{\sqrt {500} }} – \sqrt {80} $
- $5\sqrt[3]{{16}} – 3\sqrt[3]{{54}} \times \sqrt[3]{5}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Aleph 11 - Volume 2 Pág. 173 Ex. 11
Enunciado
Resolva, em $\mathbb{R}$, as seguintes equações:
- ${x^4} = 625$
- ${x^3} = – 125$
- ${x^4} + 81 = 0$
- ${x^3} – 343 = 0$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Aleph 11 - Volume 2 Pág. 173 Ex. 10
Enunciado
Resolva, em $\mathbb{R}$, as seguintes equações:
- $x + \sqrt {2x} = 0$
- $x + 3 – \sqrt {2x – 6} = 0$
- $\sqrt {1 – x} + \sqrt {2x} = 0$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 209 Ex. 99
Enunciado
A Patrícia, usando o GeoGebra, construiu os gráficos das funções perímetro e área do triângulo [OBD], como mostra a figura.
O ponto D é um ponto móvel sobre a semicircunferência, cujo diâmetro mede 4 cm, e x é o comprimento de [BD].
- A Patrícia esqueceu-se de identificar as funções.
Qual da funções, f ou g, é o perímetro e qual delas é a área?
Identifique-as, usando argumentos baseados na figura.
- Escreva as correspondentes expressões analíticas e,
…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 94
Enunciado
Considere as funções definidas em $\mathbb{R}$ por:
| $f(x)=\frac{3x}{{{x}^{2}}-4}$ |
$f(x)=\frac{{{x}^{2}}}{x+2}$ |
$f(x)=\sqrt{{{x}^{2}}-4}$ |
| $f(x)=\left| {{x}^{2}}-4 \right|$ |
$f(x)=\frac{{{x}^{2}}-4}{{{x}^{2}}}$ |
$f(x)=\frac{{{x}^{3}}}{{{x}^{2}}-9}$
|
- Determine o domínio das funções dadas.
- Calcule, para cada uma delas: $f(-x)$, $f(x-2)$ e $-f(x)$.
- Algumas das funções é par? E ímpar?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 208 Ex. 93
Enunciado
A função polinomial definida por $f(x)={{x}^{4}}$ não é injetiva.
Encontre uma restrição g da função f de modo que g seja injetiva.
Caracterize ${{g}^{-1}}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 85
Enunciado
Sendo f e g funções reais de variável real, caracterize $f\circ g$ e $g\circ f$, em cada um dos casos:
- $\begin{matrix}
f(x)=\sqrt{x} & \text{e} & g(x)={{x}^{2}}+1 \\
\end{matrix}$
- $\begin{matrix}
f(x)={{(x-1)}^{3}} & \text{e} & g(x)=\sqrt[3]{x}+1 \\
\end{matrix}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 83
Enunciado
O quadro seguinte dá-nos o sinal de uma função f, definida em $\mathbb{R}$:
Determine o domínio das funções seguintes:
- ${{f}_{1}}:x\to \frac{1}{f(x)}$
- ${{f}_{2}}:x\to \sqrt{f(x)}$
- ${{f}_{3}}:x\to \frac{1}{\sqrt{f(x)}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 82
Enunciado
Determine, em $\mathbb{R}$, o domínio das funções:
- $f:x\to \sqrt{-x}$
- $g:x\to \sqrt{\frac{x-3}{x-4}}$
- $h:x\to \sqrt{-{{x}^{2}}+4x}$
- $i:x\to \frac{\sqrt{x-3}}{\sqrt{x-4}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
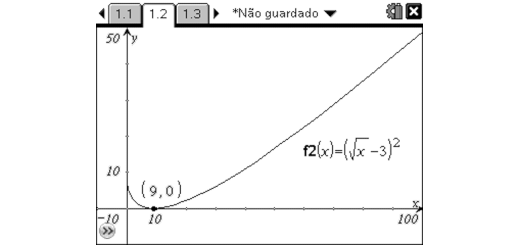
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 81
Enunciado
Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to {{(\sqrt{x}+3)}^{2}} & \text{e} & g:x\to {{(\sqrt{x}-3)}^{2}} \\
\end{matrix}\]
- Determine o domínio de f e de g.
- Determine, se existirem, os zeros de f e de g.
- Caracterize as funções $(f+g)$ e $(f\times g)$ e apresente as expressões de $(f+g)(x)$ e $(f\times g)(x)$ na forma mais simplificada possível.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 205 Ex. 80
Enunciado
Verifique se são iguais as funções reais de variável real, f e g, assim definidas:
- $\begin{matrix}
f:x\to \sqrt{{{(-x)}^{2}}} & {} & g:x\to \left| x \right| \\
\end{matrix}$
- $\begin{matrix}
f:x\to \sqrt{x}.\sqrt{x} & {} & g:x\to x \\
\end{matrix}$
- $\begin{matrix}
f:x\to \sqrt{x+1}.\sqrt{x-1} & {} & g:x\to \sqrt{{{x}^{2}}-1} \\
\end{matrix}$
Resolução >>
Resolução
<< Enunciado…
Ler mais























![Um triângulo [ABC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2017/10/9V1Pag040-1_520x245.png)





