Escola Secundária/3 da Sé-Lamego
Ficha de
Trabalho de Matemática
Ano Lectivo 2003/04 Menecmo e as secções
cónicas
10.º Ano
Sugestões
|
Sugestão
A
|
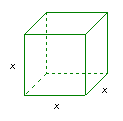
Recapitula
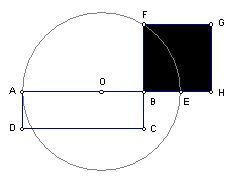
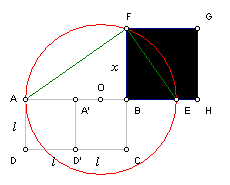
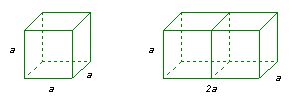
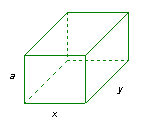
as questões B, C e D da ficha de trabalho intitulada "Da duplicação
do quadrado à redução de Hipócrates”, em:
http://www.prof2000.pt/users/amma/af18/t5/FT-4.htm
FIM
(Retrocede)
|
|
Sugestão
B
|
Será importante ter presente as
questões B e C da ficha de trabalho "Da duplicação do quadrado à
redução de Hipócrates”, em:
http://www.prof2000.pt/users/amma/af18/t5/FT-4.htm
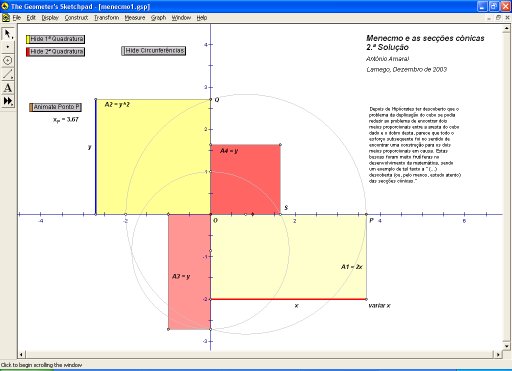
A exploração do sketch
GSP pode ajudar a resolver a questão indicada.
Tem presente que dos 4 quadriláteros, dois são quadrados e dois são rectângulos.
Ficheiro GSP (versão
4)
FIM
(Retrocede)
|
|
Sugestão
C
|
Não esqueças as relações
consideradas na questão anterior.
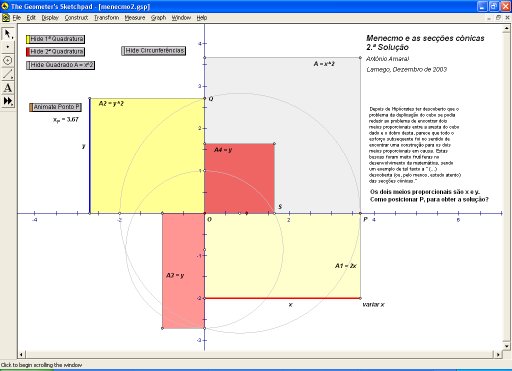
A exploração do sketch
GSP, pode ajudar a resolver a questão indicada.
Tem presente que dos 5 quadriláteros, três são quadrados e dois são rectângulos.
Ficheiro GSP (versão
4)
FIM
(Retrocede)
|
|
Sugestão
D
|
A primeira parte da questão é muito simples: basta,
dessa dupla igualdade, considerar as três proporções possíveis de escrever
e resolvê-las em ordem à variável adequada.
A resolução gráfica apresentada no texto introdutório
desta ficha de trabalho corresponde à seguinte imagem:
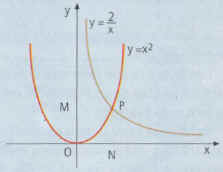
Temos, portanto, que considerar as
funções [A] e [B] (no contexto de problema, os domínios
dessas funções são R+, mas de momento não nos iremos preocupar
com isso), que depois de introduzidas no menu de gráfico das calculadoras e
de uma escolha adequada para a janela de visualização, poder-se-á obter:
 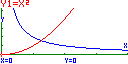
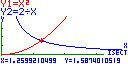
Tendo-se obtido x = 1,26 (2 c.d.).
FIM
(Retrocede)
|
|
Sugestão
E
|
O pequeno problema é que não é
possível introduzir a expressão [C] no modo de gráficos da
calculadora, como já deves ter verificado.
Mas, como sabes,
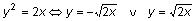
e, no contexto do problema, x
e y são dois valores positivos.
Então qual será a segunda função
que se deve considerar?
Depois de introduzidas as funções
adequadas no menu de gráfico das calculadoras e de uma escolha adequada para
a janela de visualização, poder-se-á obter:
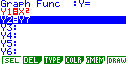
 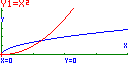
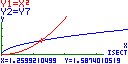
De novo, obtém-se x = 1,26 (2 c.d.).
FIM
(Retrocede)
|
|
Sugestão
F
|
Explora o sketch
GSP.
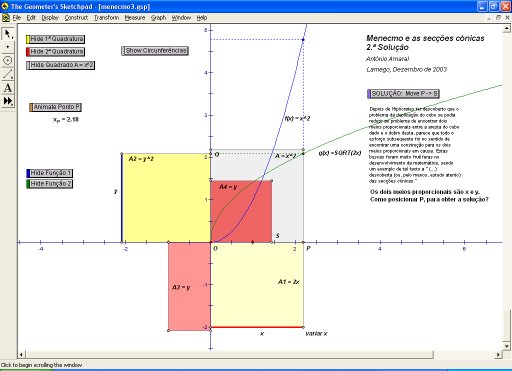
Ficheiro GSP (versão
4)
A que elementos geométricos se pode fazer
corresponder cada uma das funções?
FIM
(Retrocede)
|
|
Sugestão
G
|
Em caso de necessidade, explora o sketch
GSP.
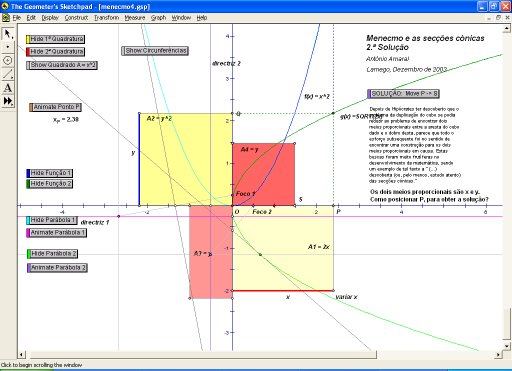
Ficheiro GSP (versão
4)
FIM
(Retrocede)
|
|
Sugestão
H
|
Para responder às questões formuladas, interpreta e
relaciona as informações fornecidas a seguir:
A parábola como lugar geométrico
Deve-se ainda aos matemáticos gregos da antiguidade a
definição de parábola como o lugar geométrico dos pontos do plano
equidistantes de uma recta – a directriz – e de um ponto exterior
a ela – o foco.
Retirado de Infinito 10, pág.
254, Areal Editores, 1997
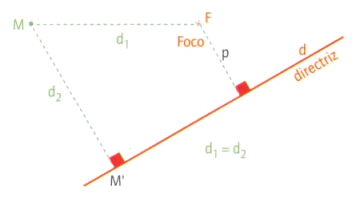
Tendo em consideração a definição dada
acima, explora a animação seguinte:
|
A
construção:
Q é um ponto livre da directriz. A recta desenhada a verde é a
mediatriz do segmento de recta [FQ]. O ponto P é a intersecção
desta mediatriz com a recta perpendicular à directriz e que contém
Q. |
|
Ficheiro GSP (versão
3) |
Qual é o lugar geométrico do plano
definido pelo ponto P, quando Q se desloca ao longo da directriz? Porquê?
A parábola definida por uma expressão analítica
Depois do contributo de Descartes com o seu método das
coordenadas e de um enorme aperfeiçoamento das notações matemáticas,
a parábola aparece definida actualmente, de preferência, como
sendo toda a linha curva plana cujos pontos têm coordenadas (x, y) que
obedecem a uma equação do tipo
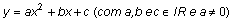
ou à equação que se obtém desta substituindo y
por x e x por y.
Também pode ser representada por uma equação da forma
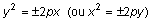
quando tem o vértice sobre a origem do referencial e um
dos eixos coordenados é seu eixo de simetria, sendo p o parâmetro
da parábola, igual à distância do foco à directriz.
A palavra “parábola”, que significa “colocação ao
lado” ou “comparação”, foi escolhida para designar a curva em
questão, dado que apresenta a seguinte propriedade: para qualquer
ponto sobre ela, a área do quadrado desenhado sobre a ordenada (abcissa)
é igual à área do rectângulo cujos lados são a abcissa (ordenada) e o
valor constante 2p.
Retirado de Infinito 10, pág.
254, Areal Editores, 1997
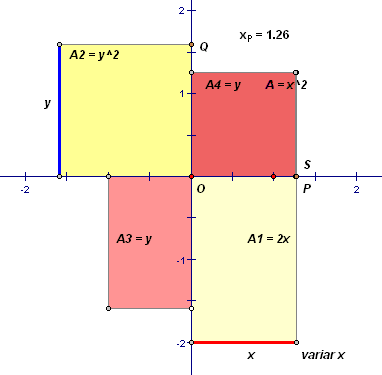
Tendo em consideração a informação dada
acima, explora a animação seguinte:
(é preferível explorar a versão GSP, pois possui maior informação)
|
Ficheiro GSP (versão
4) |
|
Toma novamente atenção à solução geométrica
apresentada nas questões B e C, assim como às caixas de texto relativas a: A
parábola como lugar geométrico e A parábola definida por uma
expressão analítica.
Explica porque é que essas construções de um certo ponto de intersecção
de duas cónicas entram na solução do problema da duplicação do cubo.
FIM
(Retrocede)
|
|